Simple Harmonic Motion

A single cycle of a sine wave can be depicted as if it were a point on a circle moving anti-clockwise (they are mathematically equivalent). At its starting point (when the sine wave is moving up from the baseline the point is at zero degrees (or zero radians: the 3 o'clock position on the circle). At the top of the sine wave's first peak it is equivalent to being at the 90° (or /2 radians: 12 o'clock) position in the circle. When the sine wave reaches the baseline on its way down it is equivalent to the 180° ( radians: 9 o'clock) position. When the sine wave reaches the bottom of the first dip it is at 270° (3 /2 radians: 6 o'clock). When it completes its first cycle it is back at the starting point 360° 0° (2 0 radians). (see attached figure)

400° is equivalent to 400°-360° = 40° and all other angles higher than 360° (2 radians) are equivalent to a value between 0° and 360°. That is, the position in a sine wave can always be referred to the equivalent position in the first cycle of that sine wave.

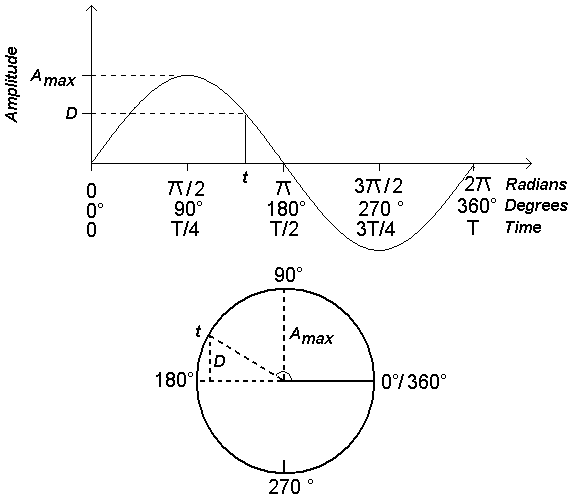
Figure 4: Simple Harmonic Motion

APPENDIX

SOME EXTRA NOTES ON SIMPLE HARMONIC MOTION

It is useful when working with formulae relating to simple harmonic motion, to understand the relationship between radians and degrees. Radians are related to degrees by the formula:-

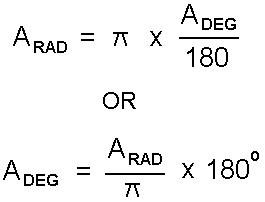
A_RAD angle in radians

A_DEG angle in degrees 3.1415927

(nb. is the ratio of the circumference over the diameter of a circle and is the same for all circles.)

When making calculations utilising the following formula for simple harmonic motion it is important to be absolutely clear whether you are using degrees or radians. Most calculators allow trigonometric (ie. sine, cosine, etc.) calculations in either degrees or radians so make sure that you know which one you are using (otherwise your result will be wrong).

The formula for simple harmonic motion is:-

a) Radians

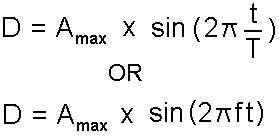
b) Degrees

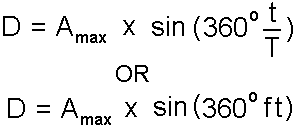
D Amplitude (pressure) at time t A_max maximum amplitude (pressure) of sine wave T period of the wave f frequency of the wave t any time that we wish to examine

Footnotes

1.  See Clark and Yallop (section 7.3) for more information